สูตรคณิตศาสตร์ ชั้นมัธยมศึกษาปีที่ 6
การจัดหมู่
หมายถึง การนำสิ่งของที่มีความแตกต่างกันทั้งหมดหรือเพียงบางส่วนมาจัดหมู่ โดยไม่ถือตำแหน่งหรือลำดับก่อนหลังเป็นสำคัญ
จำนวนวิธีจัดหมู่ของสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมด ให้มีหมู่ละ r สิ่ง (r<n หรือ r=n) เท่ากับ n! / (n-1)! . r! วิธี หรือ C(n, r) = n! / (n-1)! . r!
ตัวอย่าง มีดินสอ 12 แท่ง ซึ่งมีสีแตกต่างกันทั้งหมด ต้องการหยิบทีละ 5 แท่ง จงหาวิธีที่แต่ละครั้งในการหยิบมา จะต้องมีดินสอสีเขียวอยู่ด้วยเสมอ
วิธีทำ จากโจทย์ แสดงว่าจะสามารถเลือกหยิบสีอื่นๆ ได้อีกเพียง 4 แท่งจากปากกาทั้งหมด 11 แท่งที่เหลือ
จะได้ว่า จำนวนวิธีในการหยิบ = 11! / (11-4)! . 4! = 11 . 10 . 9 . 8 / 4 . 3 . 2 . 1 วิธี
ดังนั้น จำนวนวิธีในการหยิบ = 330 วิธี
การแบ่งสิ่งของที่แตกต่างกันทั้งหมดออกเป็นกลุ่มๆ
การแบ่งสิ่งของ n สิ่ง ซึ่งแตกต่างกันทั้งหมดออกเป็นกลุ่มๆ โดยที่
กลุ่มที่ 1 มีสิ่งของอยู่ n1 สิ่ง
กลุ่มที่ 2 มีสิ่งของอยู่ n2 สิ่ง
กลุ่มที่ 3 มีสิ่งของอยู่ n3 สิ่ง
.
.
.
กลุ่มที่ k มีสิ่งของอยู่ nk สิ่ง
เมื่อ n = n1 + n2 + n3 + … + nk
ซึ่งการแบ่งสิ่งของเหล่านี้ แบ่งเป็นกรณี ได้ดังนี้
1. ถ้าไม่มีสิ่งของในกลุ่มไหนเท่ากันเลย จำนวนวิธีที่จะแบ่งสิ่งของเหล่านี้ ทำได้ [n! / n1! . n2! . n3! . … . nk!] วิธี
2. ถ้าสิ่งของที่นั้นมีจำนวนเท่ากันทุกกลุ่ม กลุ่มละ m สิ่ง แต่ละกลุ่มมีลักษณะแตกต่างกัน จะได้จำนวนวิธีที่จะแบ่งสิ่งของ = n! / (m!)kวิธี
3. ถ้าสิ่งของมีจำนวนเท่ากันทุกกลุ่ม กลุ่มละ m สิ่ง และแต่ละกลุ่มมีลักษณะเหมือนกัน จำนวนวิธีที่จะแบ่งได้ คือ n! / (m!)k . k! วิธี
4. ถ้าจะเลือกมาจัดหมู่แต่ละประเภทเป็นจำนวน r1, r2, r3, …, rk ตามลำดับแล้ว จำนวนวิธีในการจัดหมู่ทั้งหมด เท่ากับ C(n1, r1) . C(n2, r2) . C(n3, r3) . … . C(nk, rk)
ตัวอย่าง ถ้าต้องการแบ่งขนม 40 ชิ้น ใส่ลงในถุง โดยแต่ละถุงมี 5, 7, 12 และ 16 ชิ้น จะสามารถแบ่งได้กี่วิธี
วิธีทำ จากโจทย์ ตรงตามข้อ 1
n! = 40!
n1! = 5! , n2! = 7! , n3! = 12! , n4! = 16!
ดังนั้น จำนวนวิธีที่จะแบ่งขนม ทำได้ = 40! / 5! . 7! . 12! . 16! วิธี
การแบ่งสิ่งของที่เหมือนกันทั้งหมดออกเป็นกลุ่มๆ
แบ่งเป็นกรณีได้ ดังนี้
1. กำหนดให้มีสิ่งของ n สิ่ง ซึ่งเหมือนกันทั้งหมด ต้องการแบ่งให้คน 1 คน สามารถทำได้
1a. ให้อย่างน้อย 1 ชิ้น จะทำได้ทั้งหมด n วิธี
1b. ไม่ให้เลยสักชิ้น จะทำได้ n+1 วิธี
2. กำหนดให้มีสิ่งของ n สิ่ง ต้องการแบ่งให้คน r คน สามารถทำได้
2a. แต่ละคนได้รับการแบ่งคนละ n1, n2, n3, … , nr ชิ้น ตามลำดับ จะแบ่งสิ่งของทั้งหมดหรือไม่ก็ได้ จะสามารถแบ่งได้ 1 วิธี
2b. การแบ่งโดยแต่ละคนได้รับสิ่งของอย่างน้อยคนละ 1 ชิ้นและแบ่งสิ่งของให้หมดจะทำได้ C(n-1, r-1) วิธี
2c. การแบ่งสิ่งของให้หมด โดยแต่ละคนจะได้รับคนละกี่ชิ้นก็ได้ ทำได้ C(n+r-1, r-1) วิธี
ตัวอย่าง ถ้ามีดินสออยู่ 20 แท่งที่เหมือนกัน แจกให้คน 10 คน โดยจะต้องแบ่งดินสอให้ทั้งหมด และแบ่งให้คนละกี่แท่งก็ได้ (บางคนไม่ได้รับก็ได้) จะสามารถทำได้กี่วิธี
วิธีทำ จากโจทย์ จะเห็นว่า ตรงกับข้อ 2c
จำนวนวิธีแจกดินสอ = C(20+10-1, 10-1) = C(29, 9)
= 29! / (29-9)! . 9! = 29! / 20! . 9!
= 29 . 13 . 23 . 11 . 21 . 5
ดังนั้น จำนวนวิธีแจกดินสอ = 29 . 13 . 23 . 11 . 21 . 5
การเข้าคู่กันของสิ่งของที่แตกต่างกันทั้งหมด
การเข้าคู่กันของสิ่งของที่แตกต่างกัน จะพิจารณาอยู่ 4 ลักษณะ คือ
1. อะไรคู่กับอะไร
2. อะไรคู่กับอะไร และอะไรอยู่ด้านซ้าย อะไรอยู่ด้านขวา
3. อะไรคู่กับอะไร และการจัดลำดับว่าเป็นคู่ที่เท่าใด
4. อะไรคู่กับอะไร อะไรอยู่ด้านซ้าย อะไรอยู่ด้านขวา การจัดลำดับว่าเป็นคู่ที่เท่าใด
การหาจำนวนวิธีในการเข้าคู่กันของสิ่งของ แบ่งเป็นกรณี ได้ดังนี้
1. การเข้าคู่กันของสิ่งของที่แตกต่างกันทั้งสองฝ่าย โดยที่จำนวนชิ้นเท่ากัน สมมติให้มีสิ่งของที่แตกต่าง 2 ฝ่าย ฝ่ายละ n ชิ้น จำนวนวิธีในการเข้าคู่กันคือ
ลักษณะ 1 มี n! วิธี
ลักษณะ 2 มีทั้งหมด n! . 2n วิธี มาจาก
i. อะไรคู่กับอะไร มี n! วิธี
ii. อะไรอยู่ซ้าย ขวา มี 2n วิธี
ลักษณะ 3 มีทั้งหมด (n!)2 วิธี มาจาก
i. อะไรคู่กับอะไร มี n! วิธี
ii. จัดลำดับว่าเป็นคู่ที่เท่าใด มี n! วิธี
ลักษณะ 4 มีทั้งหมด 2n . (n!)2 วิธี มาจาก
i. อะไรคู่กับอะไร มี n! วิธี
ii. อะไรอยู่ซ้าย ขวา มี 2n วิธี
iii. จัดลำดับว่าเป็นคู่ที่เท่าใด มี n! วิธี
2. การเข้าคู่กันของสิ่งของที่แตกต่างกันสองฝ่าย โดยที่จำนวนชิ้นไม่เท่ากัน สมมติให้มีสิ่งของที่แตกต่างกัน 2 ฝ่าย โดยฝ่ายหนึ่งมีอยู่ n ชิ้น ส่วนอีกฝ่ายมี r ชิ้น ซึ่งในกรณีนี้ จะสามารถเข้าคู่ได้เพียง r คู่ เท่านั้น จำนวนวิธีนากรเข้าคู่กันของสิ่งของ มีดังนี้
ลักษณะ 1 มี P(n, r) วิธี
ลักษณะ 2 มีทั้งหมด P(n, r) . 2r วิธี มาจาก
i. อะไรคู่กับอะไร มี P(n, r) วิธี
ii. อะไรอยู่ซ้าย ขวา มี 2r วิธี
ลักษณะ 3 มีทั้งหมด P(n, r) . r! วิธี มาจาก
i. อะไรคู่กับอะไร มี P(n, r) วิธี
ii. จัดลำดับว่าเป็นคู่ที่เท่าใด มี r! วิธี
ลักษณะ 4 มีทั้งหมด 2r . P(n, r) . r! วิธี มาจาก
i. อะไรคู่กับอะไร มี P(n, r) วิธี
ii. อะไรอยู่ซ้าย ขวา มี 2r วิธี
iii. จัดลำดับว่าเป็นคู่ที่เท่าใด มี r! วิธี
ตัวอย่าง นักกีฬา 8 คน ต้องการจับคู่กันออกกำลังกาย จงหาจำนวนวิธีในการจับคู่ ถ้า
1. สนใจเพียงใครคู่กับใครเท่านั้น
2. สนใจวาใครคู่กับใคร และใครลงสนามด้านใดบ้าง
3. สนใจใครคู่กับใคร และลำดับคู่ที่เท่าไหร่
4. สนใจว่าใครคู่กับใคร อยู่ด้านใดของสนาม และเป็นคู่ที่เท่าไหร่
วิธีทำ
ดังนั้น
1. สนใจเพียงใครคู่กับใครเท่านั้น จะทำได้ 8! / 24 . 4! วิธี
2. สนใจวาใครคู่กับใคร และใครลงสนามด้านใดบ้าง จะทำได้ 8! / 4! วิธี
3. สนใจใครคู่กับใคร และลำดับคู่ที่เท่าไหร่ จะทำได้ 8! / 24 วิธี
4. สนใจว่าใครคู่กับใคร อยู่ด้านใดของสนาม และเป็นคู่ที่เท่าไหร่ จะทำได้ 8! วิธี
ทฤษฎีบททวินาม (Binomial Theorem)
จากสูตรการคูณสำหรับการกระจายทวินาม จะได้ว่า ทวินาม (a+b)n เมื่อ n เป็นจำนวนเต็มบวกหรือศูนย์ คือ การนำ (a+b) มาคูณกันจำนวน n วงเล็บ เช่น (a+b)4 = (a+b) . (a+b) . (a+b) . (a+b)
แต่ถ้าการกระจายนั้นมีค่า n มากๆ ก็จะทำให้หาค่าได้ยากขึ้น ดังนั้น เราจึงต้องใช้ทฤษฎีบททวินามช่วยในการกระจาย
สามเหลี่ยมของปาสคาล (Pascal’s triangle)
เมื่อพิจารณาการกระจายทวินาม (a+b)n เมื่อ n เป็นจำนวนเต็มบวกหรือศูนย์ จะได้
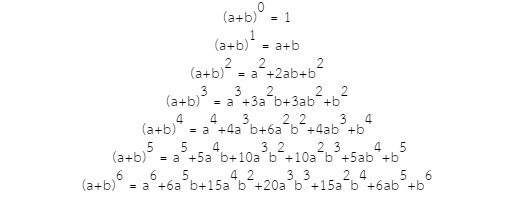

แผนภาพนี้เรียกว่า “สามเหลี่ยมของปาสคาล”
จากสามเหลี่ยมปาสคาล ทำให้เราทราบว่า
1. จำนวนแรกและจำนวนสุดท้ายของแต่ะแถมเท่ากับ 1 เสมอ
2. จำนวนใดๆ ในแต่ละแถว เกิดจากการบวกของจำนวน 2 จำนวน ที่อยู่เหนือจำนวนนั้นๆ ไปทางซ้ายและทางขวาของแถวด้านบนที่ติดกัน
3. สามเหลี่ยมปาสคาลมีลักษณะสมมาตร
4. จำนวนทั้งหมดที่อยุ่ในแถวที่ n มีค่าเท่ากับ n+1 จำนวน
5. ผลบวกของจำนวนทุกจำนวนในแถวที่ n มีค่าเท่ากับ 2



![]()
แคลคูลัส

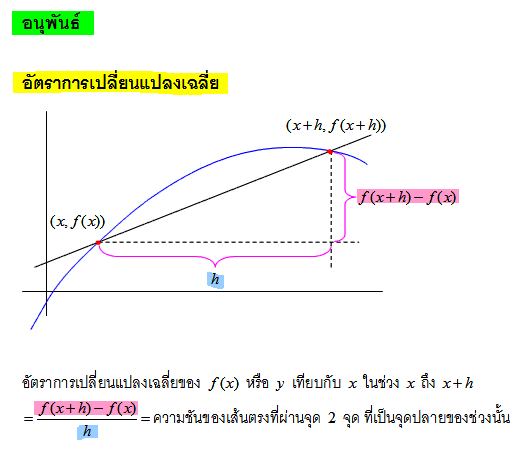




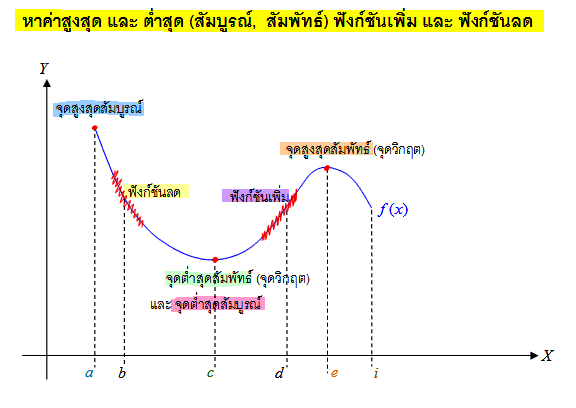




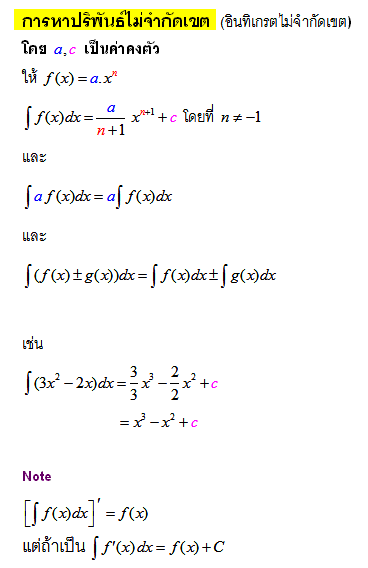



ที่มา : Tewlek.com , Scimath คลังความรู้สู่ความเป็นเลิศ , Scimath คลังความรู้สู่ความเป็นเลิศ




